oreocomputers.blogg.se - Right isosceles triangle

Let’s look at an example of a right triangle that is scalene – and then, a right triangle that is not scalene. That is, if the side lengths are a, b, and c, then a ≠ b, a ≠ c, and b ≠ c.

No two sides are the same length – by definition, the 3 sides of a scalene triangle have different lengths, so no two sides have the same length.

One angle is 90 degrees – the largest angle (the right angle) is across from the largest side (the hypotenuse), and it measures 90 degrees, by definition of a right triangle.

Here are some important things to remember about a right scalene triangle: However, not every right triangle is scalene, and not every scalene triangle is a right triangle. Can A Right Triangle Be Scalene?Ī right triangle can be scalene. Thus, it is not isosceles, since all 3 sides have different lengths. This right triangle has side lengths 3, 4, and 5 (a Pythagorean Triple satisfying the equation a 2 + b 2 = c 2).

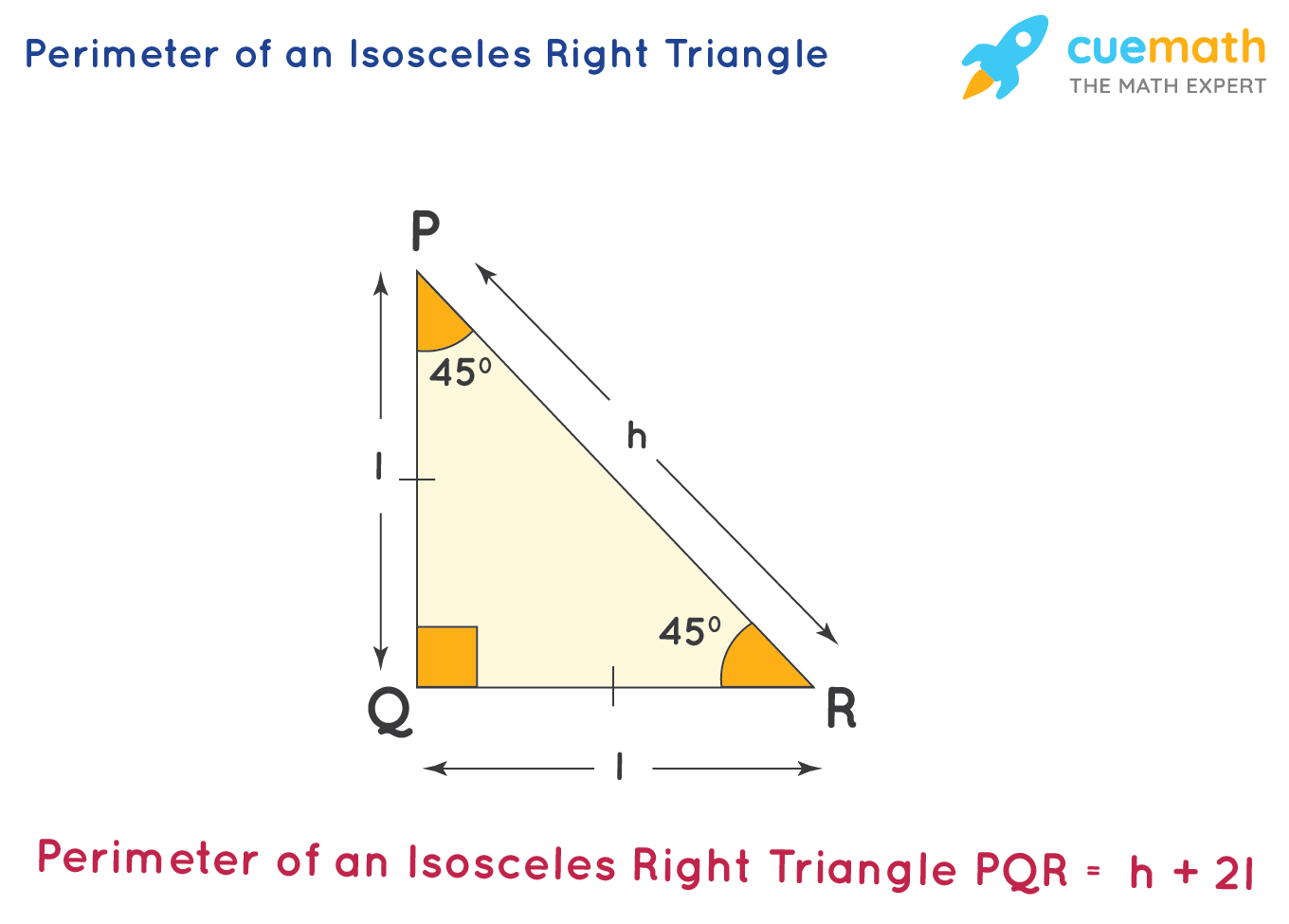
Note: this means that all right isosceles triangles are similar. So, if the shortest side of an isosceles triangle has a length of 10 feet, then the longest side (the hypotenuse) has a length of 10√2 feet. This gives us a specific ratio of side lengths: 1:1:√2. This tells us that a right isosceles triangle has angles 45-45-90. Thus, the two smaller angles in a right isosceles triangle have a measure of 45 degrees. Then, recall that the two smaller angles have the same measure. Next, remember that the largest angle is 90 degrees (let’s say that angle is z). Now let’s prove that the two smaller angles in a right isosceles triangle are 45 degrees.įirst, remember that the three angles in any triangle add up to 180 degrees. As it turns out, their measure is 45 degrees (there is a proof of this below). Two angles have the same measure of 45 degrees – the two smallest angles (across from the legs) of the triangle have the same measure, since their opposite sides have the same length.The sides satisfy the equation for a Pythagorean Triple – since we have a right triangle, the side lengths a, b, and c of a right scalene triangle satisfy the equation a 2 + b 2 = c 2, which comes from the Pythagorean Theorem.Two sides are the same length – the two shortest sides (the legs) of the triangle have the same length, by definition of an isosceles triangle.Here are some important things to remember about a right isosceles triangle: However, not every right triangle is isosceles, and not every isosceles triangle is a right triangle.ĭrawing Irregular Shapes: One Point Perspective Can A Right Triangle Be Isosceles?Ī right triangle can be isosceles. Let’s answer some of those questions now. This raises certain questions about which combinations can occur. However, there are lots of different types of triangles. They are also central to trigonometry, which makes them useful in calculus as well. Right triangles come up often in geometry.

All About Right Triangles & Their Angles (7 Common Questions Answered) We’ll also see which combinations are possible and which ones are not. In this article, we’ll take a closer look at some different types of right triangles. Of course, it takes some work to think through questions about triangles and to prove these concepts. However, every pair of equilateral triangles or right isosceles triangles are similar. Two right triangles can be similar, but not every pair of right triangles is similar. So, what do you need to know about right triangles and their angles? Some right triangles are isosceles or scalene, but no right triangle is equilateral, acute, or obtuse. Right triangles are important in many area of mathematics, including geometry, trigonometry, and calculus (that’s just for starters!) However, there are lots of questions that you might have about right triangles.