
Educators earn digital badges that certify knowledge, skill, and experience.
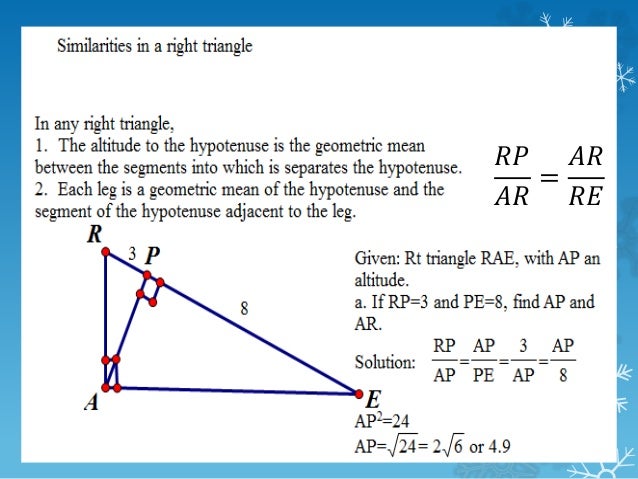
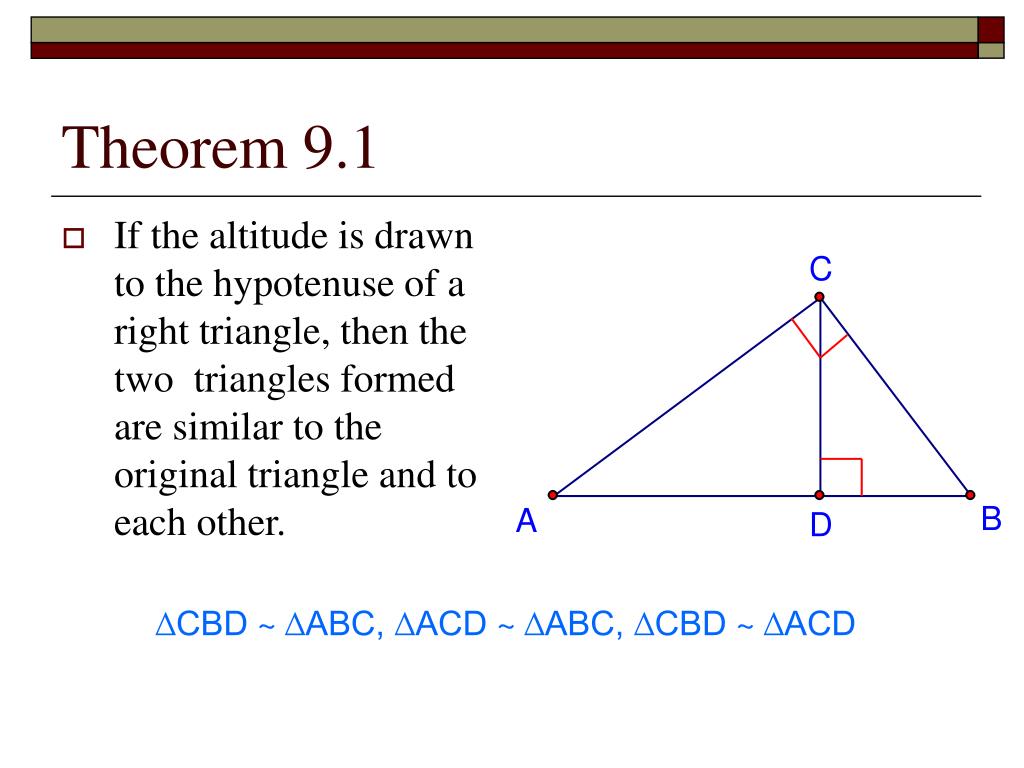
Save time lesson planning by exploring our library of educator reviews to over 550,000 open educational resources (OER).Īn all-in-one learning object repository and curriculum management platform that combines Lesson Planet’s library of educator-reviews to open educational resources with district materials and district-licensed publisher content.Ī comprehensive online edtech PD solution for schools and districts. Timely and inspiring teaching ideas that you can apply in your classroom Standard 1.02 & 2.03: 1: The learner will perform operations with real numbers to solve problems. In the below example, we can see CBD ABC, ACD ABC, and CBD ACD. Manage saved and uploaded resources and foldersīrowse educational resources by subject and topic If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and to each other. Let triangle ABD and ECD be similar triangles.Īpply the Side-Angle-Side (SAS) rule, where A = 90 degrees.Search reviewed educational resources by keyword, subject, grade, type, and more Let’s check if the proportions of the corresponding two sides of the triangles are equal.Ĭheck whether the two triangles shown below are similar and calculate the value k.īy Side-Angle-Side (SAS) rule, the two triangles are similar.ĭetermine the value of x in the following diagram. Recall that an altitude of a triangle is a perpendicular line segment from a vertex to the line. Given that the two triangles are similar, then Similarity: Right triangles, altitudes, and similarity.

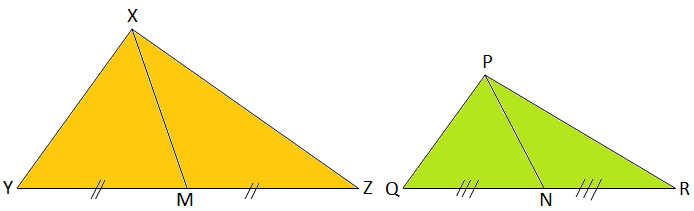
Sum of interior angles in a triangle = 180°įind the value of x in the following triangles if, ΔWXY~ΔPOR. Example: Write a similarity statement relating the three triangles in each diagram. Let’s take a look at the following examples:Ĭheck whether the following triangles are similar There are two types of similar triangle problems these are problems that require you to prove whether a given set of triangles are similar and those that require you to calculate the missing angles and side lengths of similar triangles. Two triangles are similar if all the corresponding three sides of the given triangles are in the same proportion. The SAS rule states that two triangles are similar if the ratio of their corresponding two sides is equal and also, the angle formed by the two sides is equal. With the AA rule, two triangles are said to be similar if two angles in one particular triangle are equal to two angles of another triangle. There are three rules for checking similar triangles: AA rule, SAS rule, or SSS rule. To find the geometric mean of two numbers, just find the product of those numbers and take the square root Follow along with this tutorial to learn the process. These are postulates or the rules used to check for similar triangles. The altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle. We can prove similarities in triangles by applying similar triangle theorems. Now, what does that do for us Well, that tells us that the ratio of corresponding sides are going to be the same. And then, vertex B right over here corresponds to vertex D. The ratio of all the corresponding sides in similar triangles is consistent.Įach pair of corresponding angles are equal. So we know triangle ABC is similar to triangle- so this vertex A corresponds to vertex E over here.
The ratio of corresponding sides is congruent triangles is always equal to a constant number 1. Therefore, ΔABC ~ΔPQR~ΔXYZ Comparison between similar triangles and congruent triangles Features The ratio of their corresponding sides is equal.ĪB/PQ = AC/PR= BC= QR, AB/XY= AC/XZ= BC/YZ.Similar triangles are two or more triangles with the same shape, equal pair of corresponding angles, and the same ratio of the corresponding sides. The concept of similar triangles and congruent triangles are two different terms that are closely related. Similar Triangles: Two triangles are called similar if the ratios obtained using corresponding sides. In this article, we will learn about similar triangles, features of similar triangles, how to use postulates and theorems to identify similar triangles, and lastly, how to solve similar triangle problems. The side opposite the right angle is called the hypotenuse and the other sides are called legs. Now that we are done with the congruent triangles, we can move on to another concept called similar triangles. This investigation is a great demonstration to help students visualize similar right triangles To begin, start with a regular sheet of paper.
Similar Triangles – Explanation & Examples


 0 kommentar(er)
0 kommentar(er)
